Application
CHARACTERIZATION OF 3D STRUCTURES
Driven by the continued demand for increased functionality in integrated circuits, the trend toward ever-higher levels of integration has resulted the use of increasingly three-dimensional structures in order to gain more functions out of a given area. This is evident in several areas of both device and interconnect technology. One example is the continuing trend toward higher aspect ratios in vias, contacts and memory capacitor structures. On a much larger length scale, the use of through-silicon via (TSV) structures to create 3D interconnects enables vertical stacking of multiple dies. Each of these three developments leads to new challenges in process control and metrology, and a common theme is required between them to measure profiles and depths of etched structures. While diagnostic techniques, such as SEM, AFM and SPM play an important role in characterizing processes, optical metrology methods are highly desired, because they provide rapid measurements on product wafers, enabling routine monitoring and advanced process control.
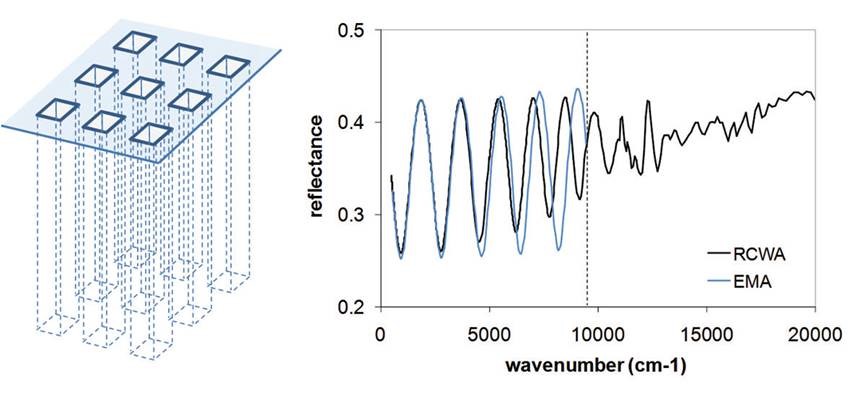
Figure 1. 3D array of square trenches in silicon (left) and corresponding simulated infrared spectra (right).





